[Algorithm] 정렬 - 병합 정렬(Merge Sort)

#요약

• 현대 컴퓨터의 아버지 '존 폰 노이만'이 제안
• 분할 정복(Divid & Conquer)의 전략을 도입
  • 문제를 작은 문제로 분리하고 각각 해결한 후에, 결과를 모아서 원래 문제를 해결하는 전략
  • 순환 호출을 구현

1. 리스트의 길이가 0 OR 1일때 이미 정렬된 것
2. 정렬되지 않는 리스트들 절반으로 잘바 비슷한 크기의 두 부분 리스트로 나눔 ➡️ Divid
3. 각 부분 리스트를 재귀적으로 병합 정렬을 이용해 정렬 ➡️ Conquer
4. 두 부분 리스트를 다시 하나의 정렬된 리스트로 병합 ➡️ Combine

#구체적 설명

1. 하나의 데이터 배열을 균등하게 절반으로 나눈다.
2. 나누어진 2개의 배열을 정렬한다.
   1. 분할: 입력 배열을 2개의 부분 배열로 분할한다.
   2. 정복: 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않을때 다시 분할한다.
   3. 결합: 분할되어 정렬된 데이터들을 합친다.
3. 이 과정을 반복한다.

#알고리즘

https://www.google.com/url?sa=i&url=https%3A%2F%2Fwww.programiz.com%2Fdsa%2Fmerge-sort&psig=AOvVaw2zh_TYFnT2hyabe15TQKXa&ust=1700028965809000&source=images&cd=vfe&opi=89978449&ved=0CA8QjRxqFwoTCMjul8frwoIDFQAAAAAdAAAAABAD

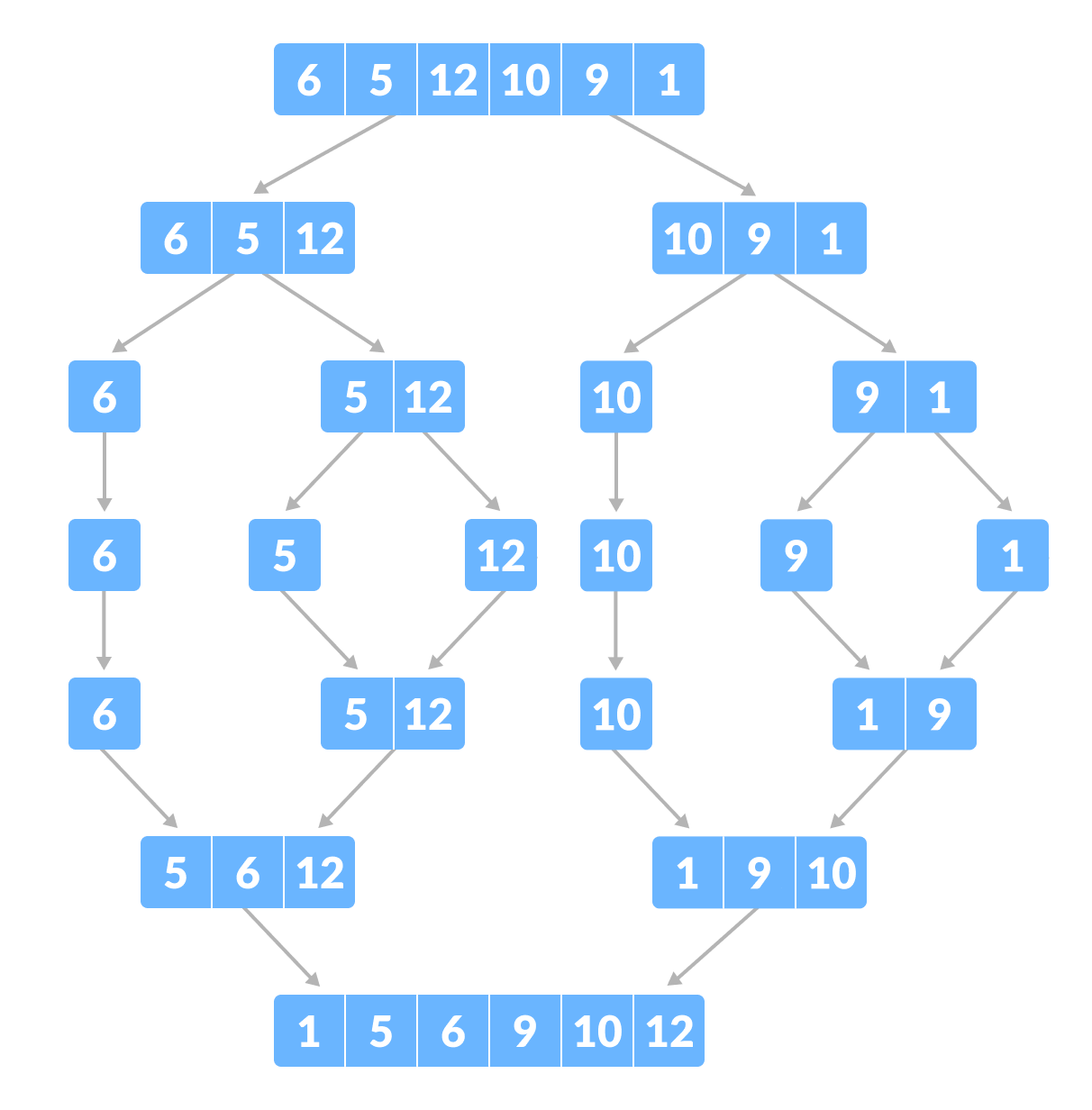
#코드 작성

public class main
{
    static int[] arr  = new int[]{7,5,2,4,0,3,6,1};
    public static void main(String[] args)
    {
        mergeSort(arr,0 ,arr.length);
        for(int i = 0 ; i < arr.length ; i++){
            System.out.printf("%d ", arr[i]);
        }
    }

    static void mergeSort(int[] arr,int low,int high){
       if (high - low < 2) { //0,1 까지 분할
            return;
        }
        int mid = (low + high) / 2;
        mergeSort(arr, 0, mid); //재귀로 분할
        mergeSort(arr, mid, high); //재귀로 분할
        merge(arr, low, mid, high); //병합
    
    }

    //병합함수
    static void merge(int list[], int low, int mid, int high){
        int[] temp = new int[high - low]; //복사하기 위한 함수 생성
        int t = 0, l = low, h = mid; 

        while (l < mid && h < high) {
            if (arr[l] < arr[h]) {
                temp[t++] = arr[l++];
            } else {
                temp[t++] = arr[h++];
            }
        }

        while (l < mid) {
            temp[t++] = arr[l++];
        }

        while (h < high) {
            temp[t++] = arr[h++];
        }

        for (int i = low; i < high; i++) {
            arr[i] = temp[i - low];
        }
    }
}

#결과

0 1 2 3 4 5 6 7

#시간복잡도

최선	O(nlogn)
평균	O(nlogn)
최악	O(nlogn)

#장단점

장점	단점
- 최선, 최악, 평균이 모두 O(nlogn) 으로 동일하다. - 제자리 정렬중 선택 정렬, 삽입 정렬 보다 효율적이다.	- 데이터를 저장하기 위한 추가적인 저장공간이 필요하다. - 데이터가 크기가 큰 경우 이동횟수가 많으므로 시간 비

---

※ 분할 정복(Divid & Conquer) 전략

• 가장 유명한 알고리즘 디자인 패러다임
• 큰 문제를 작은 문제로 쪼개서 해결하는 기법
• 주어진 문제를 둘 이상의 부분 문제로 나누고 각 문제를 해결
• 선형적인 방법보다 빠르게 문제를 해결 가능